during what intervals of time is the particle moving to the left? give a reason for your answer.
iii. Derivatives
3.4 Derivatives as Rates of Change
Learning Objectives
- Decide a new value of a quantity from the old value and the amount of alter.
- Summate the average rate of change and explain how it differs from the instantaneous rate of alter.
- Utilize rates of alter to displacement, velocity, and acceleration of an object moving along a straight line.
- Predict the future population from the present value and the population growth charge per unit.
- Use derivatives to summate marginal cost and revenue in a business organization situation.
In this section we look at some applications of the derivative by focusing on the estimation of the derivative equally the rate of change of a part. These applications include acceleration and velocity in physics, population growth rates in biological science, and marginal functions in economics.
Move along a Line
Some other use for the derivative is to analyze motion along a line. We have described velocity as the charge per unit of change of position. If nosotros take the derivative of the velocity, we tin notice the acceleration, or the rate of change of velocity. Information technology is also important to introduce the idea of speed, which is the magnitude of velocity. Thus, we can country the following mathematical definitions.
Definition
Let ![]() be a function giving the position of an object at time
be a function giving the position of an object at time ![]() .
.
The velocity of the object at fourth dimension ![]() is given by
is given by ![]() .
.
The speed of the object at time ![]() is given by
is given by ![]() .
.
The dispatch of the object at ![]() is given by
is given by ![]() .
.
Comparing Instantaneous Velocity and Boilerplate Velocity
A ball is dropped from a top of 64 anxiety. Its height above ground (in feet) ![]() seconds afterwards is given by
seconds afterwards is given by ![]() .
.

- What is the instantaneous velocity of the ball when information technology hits the ground?
- What is the average velocity during its autumn?
Position and Velocity
The position of a particle moving forth a coordinate axis is given by ![]() .
.
- Detect
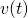 .
. - At what fourth dimension(due south) is the particle at remainder?
- On what fourth dimension intervals is the particle moving from left to right? From right to left?
- Apply the information obtained to sketch the path of the particle forth a coordinate axis.
Population Change
In addition to analyzing velocity, speed, acceleration, and position, we can use derivatives to analyze various types of populations, including those as various every bit bacteria colonies and cities. We can apply a electric current population, together with a growth charge per unit, to estimate the size of a population in the future. The population growth charge per unit is the rate of modify of a population and consequently tin can be represented past the derivative of the size of the population.
Definition
If ![]() is the number of entities present in a population, so the population growth rate of
is the number of entities present in a population, so the population growth rate of ![]() is divers to be
is divers to be ![]() .
.
Estimating a Population
The population of a city is tripling every v years. If its current population is ten,000, what volition be its approximate population ii years from now?
Solution
Let ![]() be the population (in thousands)
be the population (in thousands) ![]() years from now. Thus, we know that
years from now. Thus, we know that ![]() and based on the information, we anticipate
and based on the information, we anticipate ![]() . Now gauge
. Now gauge ![]() , the current growth charge per unit, using
, the current growth charge per unit, using
![]() .
.
By applying (Effigy) to ![]() , we tin can approximate the population 2 years from now by writing
, we tin can approximate the population 2 years from now by writing
![]() ;
;
thus, in two years the population will be approximately xviii,000.
Changes in Cost and Revenue
In addition to analyzing motility along a line and population growth, derivatives are useful in analyzing changes in cost, revenue, and profit. The concept of a marginal function is common in the fields of business and economics and implies the use of derivatives. The marginal toll is the derivative of the price function. The marginal revenue is the derivative of the acquirement function. The marginal profit is the derivative of the profit office, which is based on the cost function and the revenue function.
Nosotros can roughly approximate
![]()
by choosing an appropriate value for ![]() . Since
. Since ![]() represents objects, a reasonable and small value for
represents objects, a reasonable and small value for ![]() is 1. Thus, by substituting
is 1. Thus, by substituting ![]() , we go the approximation
, we go the approximation ![]() . Consequently,
. Consequently, ![]() for a given value of
for a given value of ![]() can be thought of as the change in cost associated with producing i additional particular. In a similar style,
can be thought of as the change in cost associated with producing i additional particular. In a similar style, ![]() approximates the revenue obtained by selling one additional item, and
approximates the revenue obtained by selling one additional item, and ![]() approximates the profit obtained by producing and selling one additional item.
approximates the profit obtained by producing and selling one additional item.
Applying Marginal Acquirement
Assume that the number of barbeque dinners that tin can exist sold, ![]() , tin be related to the price charged,
, tin be related to the price charged, ![]() , by the equation
, by the equation ![]() .
.
In this case, the acquirement in dollars obtained by selling ![]() barbeque dinners is given past
barbeque dinners is given past
![]() for
for ![]() .
.
Use the marginal acquirement function to estimate the revenue obtained from selling the 101st barbeque dinner. Compare this to the bodily acquirement obtained from the sale of this dinner.
Solution
First, detect the marginal revenue function: ![]() .
.
Next, employ ![]() to approximate
to approximate ![]() , the revenue obtained from the sale of the 101st dinner. Since
, the revenue obtained from the sale of the 101st dinner. Since ![]() , the acquirement obtained from the auction of the 101st dinner is approximately $three.
, the acquirement obtained from the auction of the 101st dinner is approximately $three.
The actual revenue obtained from the sale of the 101st dinner is
![]() , or
, or ![]() .
.
The marginal revenue is a adequately adept estimate in this case and has the advantage of being easy to compute.
Suppose that the profit obtained from the auction of ![]() fish-fry dinners is given by
fish-fry dinners is given by ![]() . Utilize the marginal profit role to gauge the profit from the sale of the 101st fish-fry dinner.
. Utilize the marginal profit role to gauge the profit from the sale of the 101st fish-fry dinner.
Key Concepts
- Using
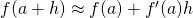 , it is possible to gauge
, it is possible to gauge 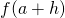 given
given 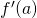 and
and 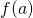 .
. - The rate of change of position is velocity, and the rate of change of velocity is dispatch. Speed is the absolute value, or magnitude, of velocity.
- The population growth rate and the nowadays population tin exist used to predict the size of a future population.
- Marginal toll, marginal acquirement, and marginal turn a profit functions can be used to predict, respectively, the price of producing ane more item, the revenue obtained past selling one more detail, and the profit obtained by producing and selling one more than detail.
For the post-obit exercises, the given functions stand for the position of a particle traveling forth a horizontal line.
- Find the velocity and acceleration functions.
- Determine the time intervals when the object is slowing downwardly or speeding upwardly.
1. ![]()
ii. ![]()
3. ![]()
Solution
a. ![]()
b. ![]()
5.A ball is thrown downward with a speed of viii ft/due south from the top of a 64-foot-tall building. After ![]() seconds, its superlative above the basis is given past
seconds, its superlative above the basis is given past ![]() .
.
- Decide how long information technology takes for the ball to hit the footing.
- Determine the velocity of the ball when information technology hits the footing.
[reveal-reply q="875579″]Show Solution[/reveal-answer]
[hidden-answer a="875579″]a. v ft/s b. nine ft/s
eight.A potato is launched vertically upward with an initial velocity of 100 ft/s from a potato gun at the top of an 85-foot-tall building. The distance in feet that the potato travels from the ground after ![]() seconds is given past
seconds is given past ![]() .
.
- Find the velocity of the murphy after 0.5 sec and five.75 sec.
- Find the speed of the spud at 0.5 sec and 5.75 sec.
- Make up one's mind when the murphy reaches its maximum acme.
- Find the acceleration of the potato at 0.5 s and 1.v s.
- Determine how long the potato is in the air.
- Determine the velocity of the potato upon hitting the footing.
ten.The post-obit graph shows the position ![]() of an object moving forth a directly line.
of an object moving forth a directly line.

- Use the graph of the position function to determine the time intervals when the velocity is positive, negative, or zero.
- Sketch the graph of the velocity function.
- Apply the graph of the velocity office to determine the time intervals when the acceleration is positive, negative, or aught.
- Determine the time intervals when the object is speeding upward or slowing downward.
eleven.The cost function, in dollars, of a company that manufactures nutrient processors is given by ![]() , where
, where ![]() is the number of food processors manufactured.
is the number of food processors manufactured.
- Find the marginal toll function.
- Find the marginal cost of manufacturing 12 food processors.
- Find the actual cost of manufacturing the thirteenth food processor.
Solution
a. ![]()
b. ![]()
c. $six per item, $0 per item
xiii. [T] A profit is earned when acquirement exceeds cost. Suppose the profit function for a skateboard manufacturer is given by ![]() , where
, where ![]() is the number of skateboards sold.
is the number of skateboards sold.
- Find the exact profit from the auction of the thirtieth skateboard.
- Detect the marginal profit function and use information technology to estimate the profit from the sale of the thirtieth skateboard.
The following questions concern the population (in millions) of London by decade in the 19th century, which is listed in the following table.
| Years since 1800 | Population (millions) |
|---|---|
| 1 | 0.8795 |
| eleven | 1.040 |
| 21 | 1.264 |
| 31 | 1.516 |
| 41 | 1.661 |
| 51 | 2.000 |
| 61 | ii.634 |
| 71 | iii.272 |
| 81 | 3.911 |
| 91 | four.422 |
18. [T]
- Using a calculator or a computer program, detect the best-fit linear function to mensurate the population.
- Find the derivative of the equation in (a) and explicate its concrete meaning.
- Detect the 2d derivative of the equation and explicate its physical meaning.
19. [T]
- Using a calculator or a reckoner program, detect the all-time-fit quadratic curve through the data.
- Observe the derivative of the equation and explain its physical significant.
- Observe the second derivative of the equation and explicate its physical pregnant.
For the following exercises, consider an astronaut on a large planet in another milky way. To learn more nearly the composition of this planet, the astronaut drops an electronic sensor into a deep trench. The sensor transmits its vertical position every second in relation to the astronaut's position. The summary of the falling sensor information is displayed in the following table.
| Time later on dropping (s) | Position (m) |
|---|---|
| 0 | 0 |
| i | −1 |
| 2 | −2 |
| 3 | −5 |
| four | −7 |
| 5 | −14 |
20. [T]
- Using a calculator or computer programme, detect the all-time-fit quadratic curve to the data.
- Discover the derivative of the position function and explain its physical meaning.
- Notice the second derivative of the position part and explain its physical significant.
21. [T]
- Using a calculator or computer programme, find the all-time-fit cubic curve to the data.
- Find the derivative of the position office and explicate its physical significant.
- Notice the second derivative of the position function and explain its physical pregnant.
- Using the consequence from (c), explain why a cubic function is not a good choice for this problem.
The following issues bargain with the Holling blazon I, II, and III equations. These equations describe the ecological event of growth of a predator population given the corporeality of prey bachelor for consumption.
Solution
a.

b. ![]() . The more increase in prey, the more growth for predators.
. The more increase in prey, the more growth for predators.
c. ![]() . Every bit the corporeality of casualty increases, the rate at which the predator population growth increases is constant.
. Every bit the corporeality of casualty increases, the rate at which the predator population growth increases is constant.
d. This equation assumes that if there is more than prey, the predator is able to increase consumption linearly. This assumption is unrealistic because we would look there to exist some saturation betoken at which at that place is too much casualty for the predator to consume adequately.
Solution
a.

b. ![]() . When the amount of casualty increases, the predator growth increases.
. When the amount of casualty increases, the predator growth increases.
c. ![]() . When the corporeality of prey is extremely modest, the rate at which predator growth is increasing is increasing, just when the amount of prey reaches to a higher place a certain threshold, the rate at which predator growth is increasing begins to subtract.
. When the corporeality of prey is extremely modest, the rate at which predator growth is increasing is increasing, just when the amount of prey reaches to a higher place a certain threshold, the rate at which predator growth is increasing begins to subtract.
d. At lower levels of prey, the prey is more easily able to avoid detection past the predator, then fewer prey individuals are consumed, resulting in less predator growth.
Source: https://opentextbc.ca/calculusv1openstax/chapter/derivatives-as-rates-of-change/